例 各位の数が異なる2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 p 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるから,909=81個 (別解) 十の位は0以外の9通り,それぞれ1の位は9通りだから,9×9=81通り 練習問題 順列と組合せの問題を混ぜました。 4 コインをn回投げたとき、表が3回連続で出ないような場合の数を$ a_n $とする。 この時の漸化式を教えてください。自然 5 なぜ黒線でひかれた範囲になるのですか?N C r の関係があるが重複順列と重複組合せなどの関係は簡単ではない. 例 各位の数が異なる2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 P 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるか

高校数学a 組分け問題全パターン 受験の月
場合の数 順列 組み合わせ 問題
場合の数 順列 組み合わせ 問題-ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ・・・」 つまり、順序が問題になるので、『順列』の考えで。 4は「男子6人、女子10人の中から男子3人、女子4人 場合の数とは 場合分けの問題を簡単に表すと 起こりうる事象の数を求める問題です。 例題) 赤玉5個、白玉3個、黄玉2個が入っている箱からボールを3個取り出すとき、 赤玉を1個だけ取り出す組み合わせは何通りあるか。



Spi練習問題 Com
場合の数の問題は大まかに分けると 順列 と 組み合わせ があり,これらは掛け算と割り算を駆使することで求めることができます. では実際に解いてみましょう! spi対策時間と距離と速さ② 対象が2人の場合 ピクニックに行った2匹を追いかけるべく、両足に力を入れ、一歩を踏み出したあるぱかさん。 果たして無事に2匹と合流し、楽しい1日をおくることができるのか。しかし、この問題も、数ある頂点の中から4つの頂点を選ぶ問題だと思えば、場合の数の学習が応用できる。 横には4つの頂点が並んでいる。 4つの頂点から2つの頂点を選ぶと、横の辺が決まる。 同じように、 縦には5つの頂点が並んでいる。
ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。 組分け(グループ分け)問題の解法 (1)区別がつくもの→区別がつくものに組み分けする方法 例題 (11)6人を部屋A、B、Cに分ける場合の数を求めよ。 但し空室があっても良いものとする。 例題 (12)同条件で空室があってはならないとする。 (2)区別が付く 場合の数を苦手とする受験生は多いです。 この分野は、目立った公式が順列の\\({}_n \\mathrm{ P }_k\\)と組み合わせの\\({}_n \\mathrm{ C }_k\\)くらいしかなく、解答方針を自力で立てないといけません。 場合の数に苦手意識を持つ人は、何でもかんでも数式と公式だけで解こうとしがち。パターンに
こんにちは、ももやまです。 今回は、 中学入試 高校入試 共通テスト(大学入試) spi(就職試験) 基本情報 など、様々な場面で出てくる場合の数、特に「順列と組み合わせの違い」に注目して説明していき順列の公式は条件付き問題になったとたん、使い方が分からなくなる人が多いです。 公式丸暗記では今後対応しきれません。 上記の仕組みをきっちり理解してください! 全場合の数がどんな樹形図になるのか明確なイメージがわけば、どんなかけ算を場合の数3|実はカンタンな円順列と数珠順列の考え方 場合の数4|組み合わせのnCrの求め方から性質まで攻略 場合の数5|同じものを含むと順列の場合の数はどう変わる? 場合の数6|重複組み合わせは2パターンでOK!←今の記事




順列と組み合わせ 算数用語集
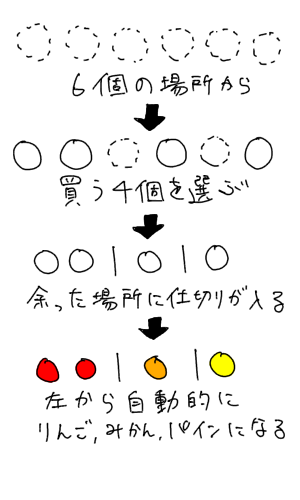



重複組み合わせは絵を描けば理解できる イラストで解説 理数白書
高校数学 問題検索 数学A 場合の数と確率 「確率の基礎」 1,754 views 高校数学 解説動画 数学A 順列 辞書式配列 1,599 views スロット雑記 ~凱旋、ハーデスを打っていて思うこ 場合の数・順列は2時間で解けるようになる 高校数学一夜漬け 目標習得時間:2時間、問題数:7問 数学が好きか嫌いかの分かれ道 場合の数は、 「並べ方」「組み合わせ」「同じものを含む」「区別する」といった曖昧な概念が登場することから、数学がとなる。 実際に、m=3 の場合に公式を適用すると、 n・ n-4 C 2 /3 となって当初の示唆に一致 することが確かめられた。 (問題補充3) 当HPがいつもお世話になっているHN「GAI」さんが、当HPの掲示板「出会 いの泉」に『微妙な違い』と題して次のような問題を出題された。




基本問題 場合の数6 同じものを含む順列と重複組み合わせ 同じものを含む順列 道順 No Youtube




Spi 場合の数 問題3 1 順列 Study Pro Spi
順列の問題(ならべ方)1 (1)男子2人に女子3人でリレーの順番を決めます。 ①全部で何通りの順番がありますか。 ②男子と女子が交互になる順番は何通りありますか。 (2)0 1 2 3の4枚のカードから3枚を並べて3けたの整数を作ります。 ①全部で何通りの整数ができますか。組合せとは いくつかのものからいくつかのものを取り出して並べることを順列と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は組合せの問題と呼ばれています. 順列 $\rightarrow$ 順序を考慮 (区別)する. 順列のまとめ数学A 場合の数の順列の問題を基本から応用までまとめます。 必要な準備和の法則と積の法則あうるさん順列の公式は和の法則と積の法則で説明できます。 足し算と掛け算が使い分けられればOKですね。 awl3nocom
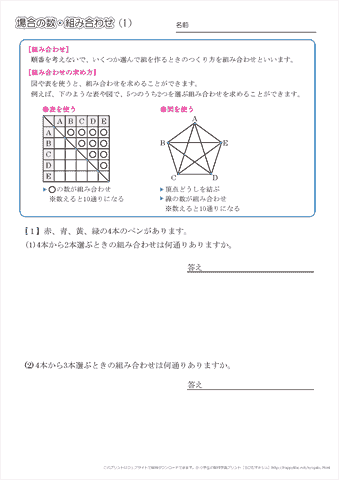



小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生
順列組合せにおける「割り算」の意味について 順列組合せの問題で「割り算」を使うことがよくあります。 例えば、 などなど。 いずれも「割り算」を行っていますが、その意味を正しく理解しているでしょうか? まずは、以下の小学生レベルの問題に全場合の数がどんな樹形図になるのか明確なイメージがわけば、どんなかけ算をすればよいのか自明になります。 異なる4枚から3枚を取り出して並べる、まさに順列の問題です。 組み合わせ公式※ これらのうち,順列と組合せには, n P r =r!




高1 数a 場合の数 4 組合せ 高校生 数学のノート Clearnote




場合の数40 完全順列1 怜悧玲瓏 高校数学を天空から俯瞰する
条件のある順列には、残念ながら 必殺技や公式 というものは存在しません。 強いていうなら、 「 条件の強いものから優先して並べろ 」です! し かし、入試問題には決まりきったパターンがあります。 条件付き順列のパターンを押さえて、その解き方やコツを覚えましょう!についてパターン別に解説していきます。 取り上げる問題はこちら! 問題①(0を含まないパターン) 6個の整数 , , , , , から異なる3個の数字を選んで3桁の整数をつくるとき,次のような数の個数を求めよ。 (1)すべての整数 (2)偶数 (3)4の この記事では「順列」と「組み合わせ」の違いや見分け方について、公式や計算問題を通してできるだけわかりやすく解説していきます。 この \\(2\\) つはよく混同されるので、この記事を通してしっかりマスターしてくださいね!




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら



こちらの問題の解答と解説を数学が得意な方にぜひお願いしたいです 場合 Yahoo 知恵袋
場合の数の勉強方法! 組み合わせと順列の解き方と勉強のコツ! 算数、数学と言っても、たいていの分野は公式を暗記することによってある程度を習得することができます。 「公式を暗記すること」と、「公式を問題に当てはめること」が比較
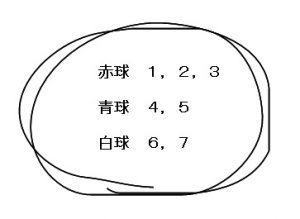



場合の数 順列と組み合わせの違いと並べ方問題の解き方




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




四谷大塚 場合の数 に苦手意識を持っているようです 中学受験 個別指導のss 1
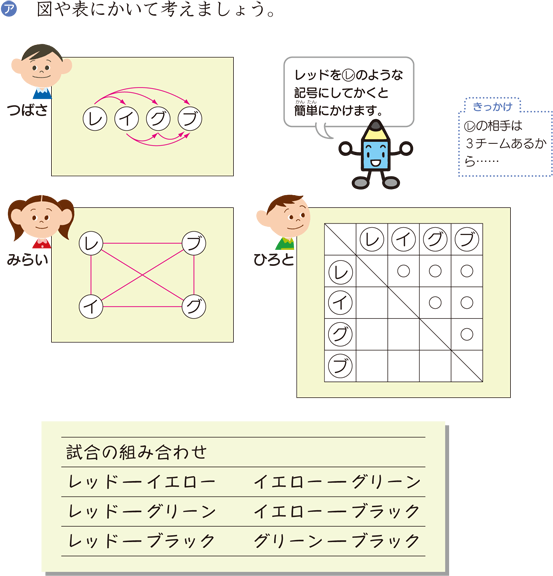



場合の数 算数用語集




中学数学 場合の数




場合の数19 円順列と数珠順列 怜悧玲瓏 高校数学を天空から俯瞰する




順列と組み合わせの公式とその違い 問題付き 理系ラボ




3講 順列 1章 場合の数と確率 問題集 高校数学a




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学



Spi練習問題 Com




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
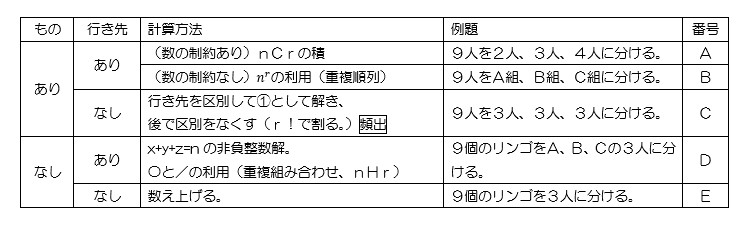



場合の数 確率を体系的に学ぼう 教科書でバラバラに登場するパターンを整理して把握しよう オンライン受講 東大に 完全 特化 東大合格 敬天塾




重複順列の応用問題 組み分けの問題 あうるさんの杜



数a順列組み合わせ 2番と3番の問題について なぜ分数になる Yahoo 知恵袋




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




高校数学 数a 7 順列 基本編 Youtube



1




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




高校数学a 順列の活用2 男女の並べ方 練習編 映像授業のtry It トライイット




重複組み合わせ は2パターンを区別すればok




組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける 計算 図 算数




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




場合の数を小学生に教えてみた 一番いい教え方を考えてはみたものの たくべや




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説




順列と組合せの違いと例題 高校数学の美しい物語



場合の数 学び家 Com




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



Spi練習問題 Com
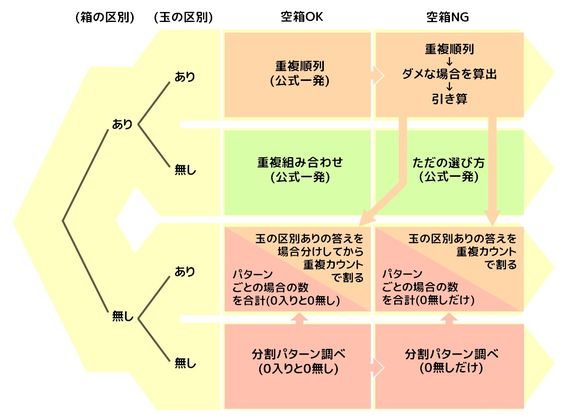



組み分け 部屋分け 問題全8パターンと解き方 数a 場合の数確率 そうちゃ S 図解英数ゼミナール




リンゴ9個 重複組合せ 解説その1 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



同じものを含む順列の問題 京極一樹の数学塾
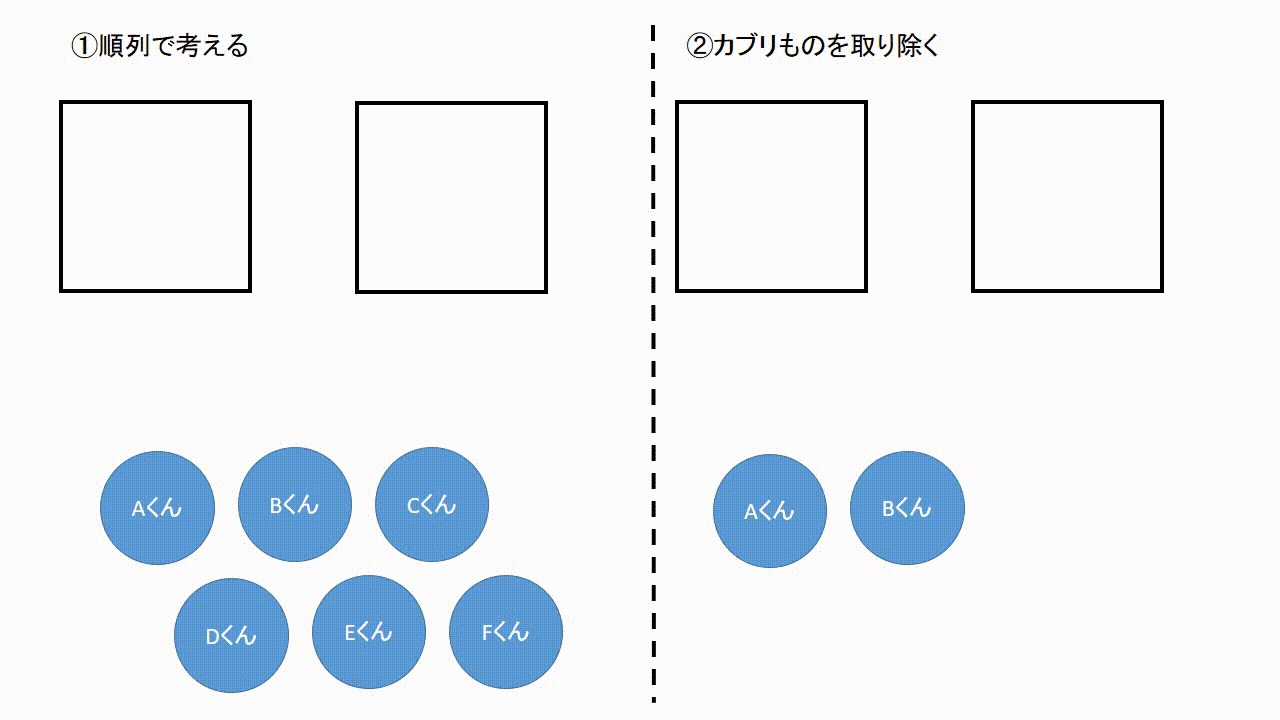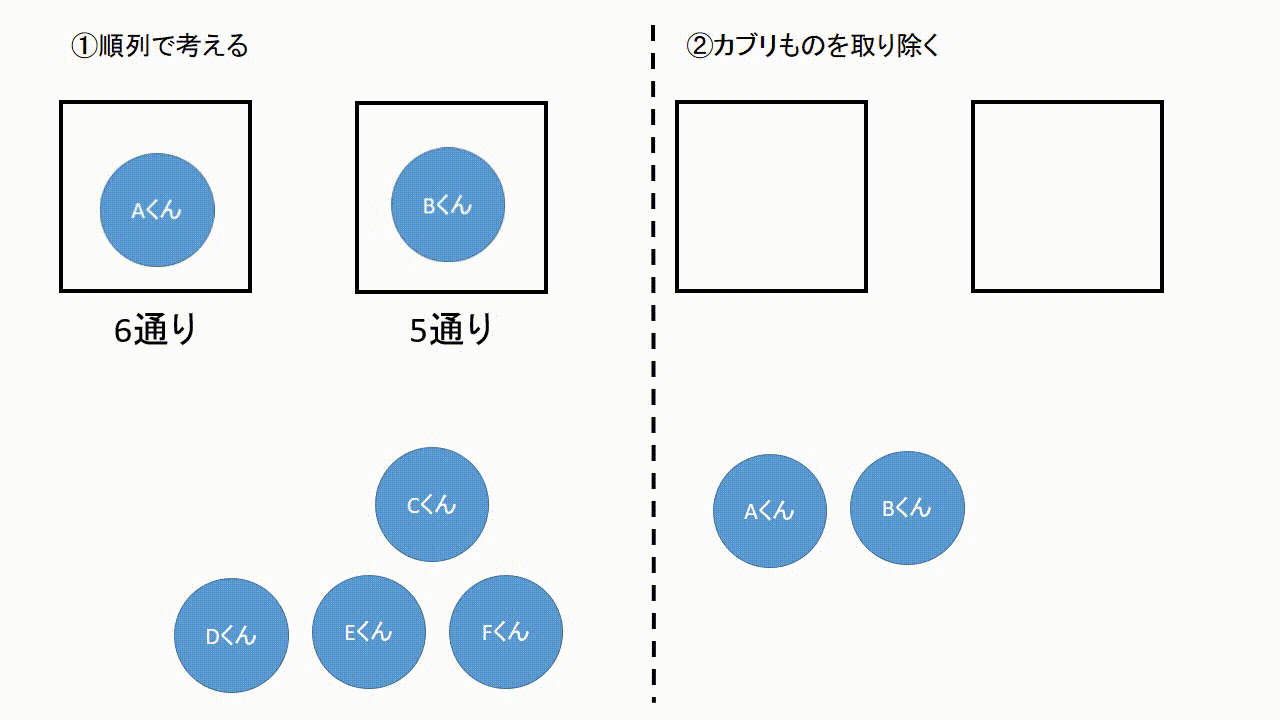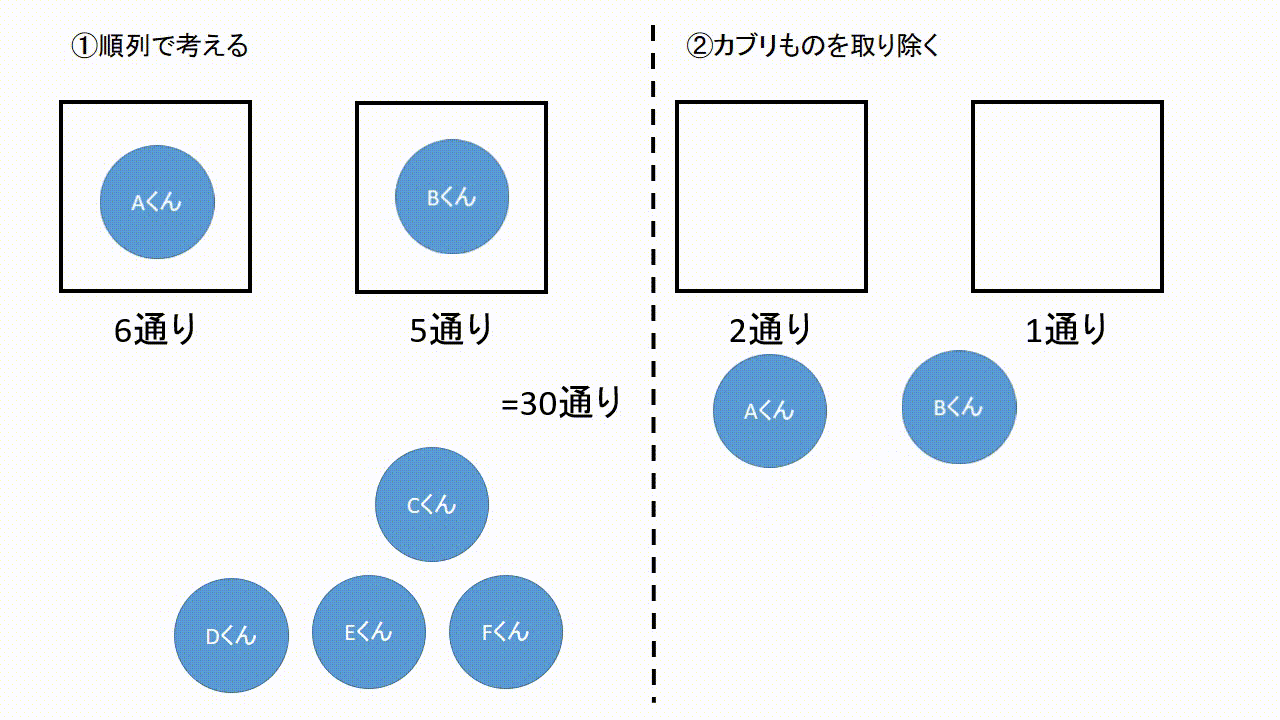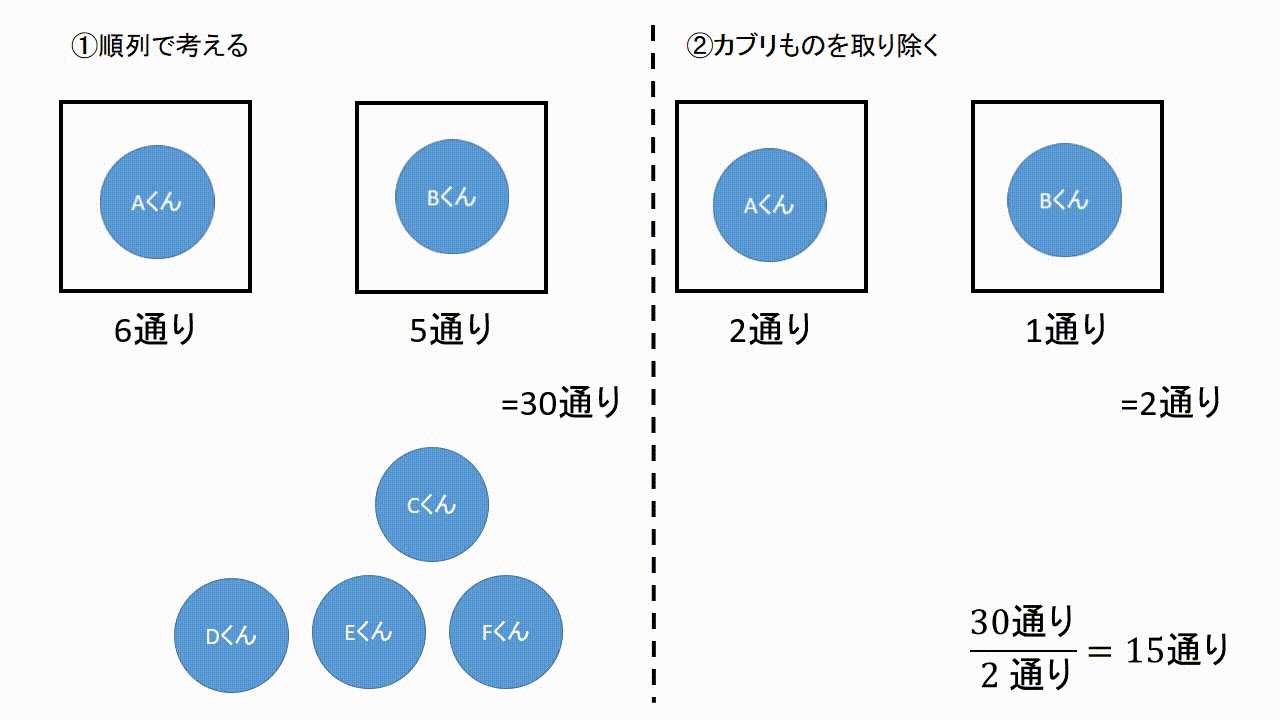



数学 確率を極めるには 場合の数 を極めろ




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




場合の数 順列 組合せ 2020年度前期日程の神戸大学文系の入試より 身勝手な主張



Spi練習問題 Com
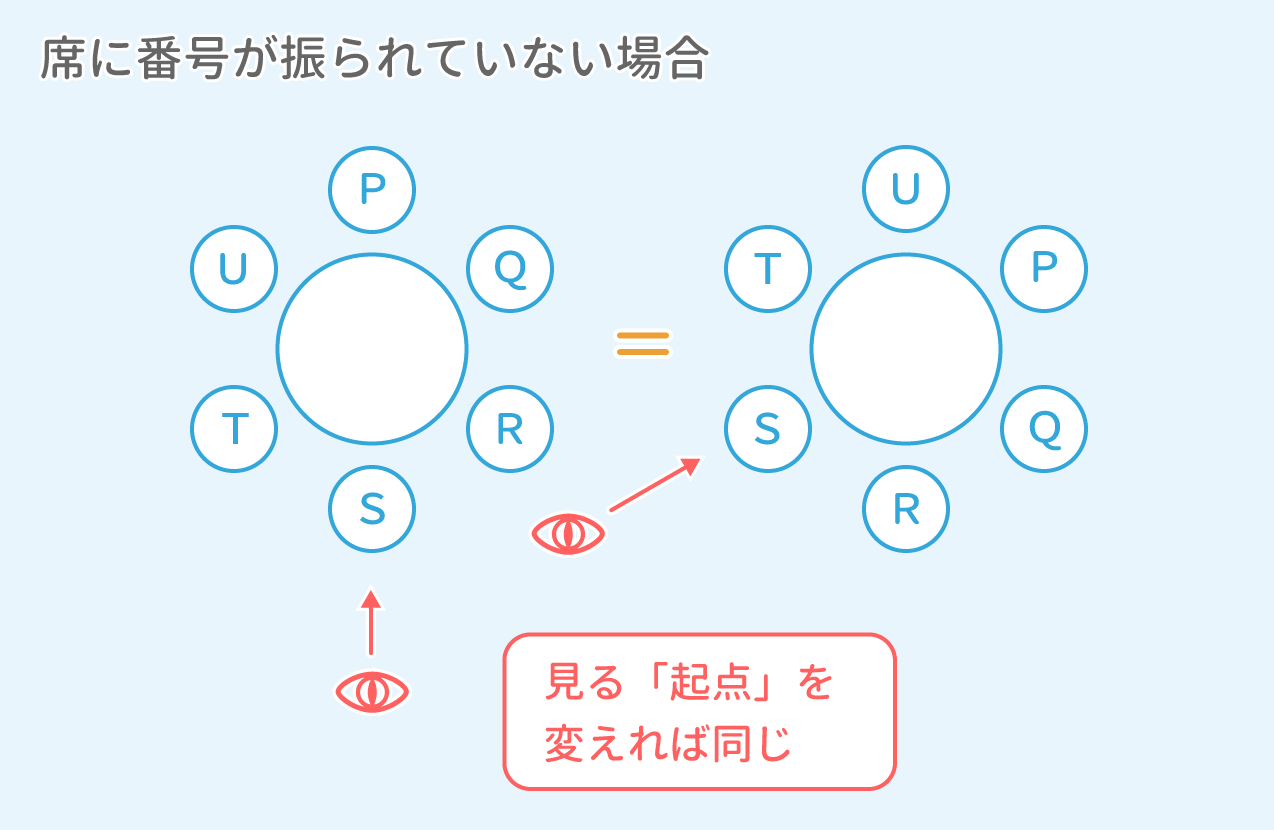



Spi 場合の数 問題4 1 円順列 Study Pro Spi




Spi 場合の数 最速解法 例題 Study Pro Spi




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




順列pと組み合わせcの違いと 簡単 な見分け方



1



3




リーグ戦とトーナメント戦 小学校6年教材より 身勝手な主張




順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん
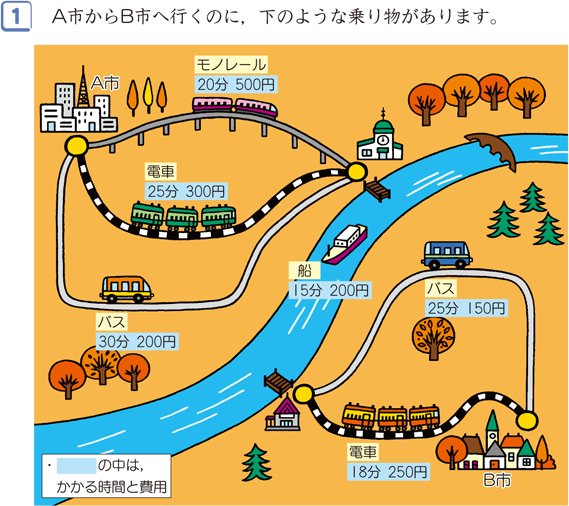



場合の数 算数用語集




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生



順列 組合せの場合の数と確率の例題 Of 京極一樹の数学塾



Spi練習問題 Com




重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ




場合の数 無料で使える中学学習プリント
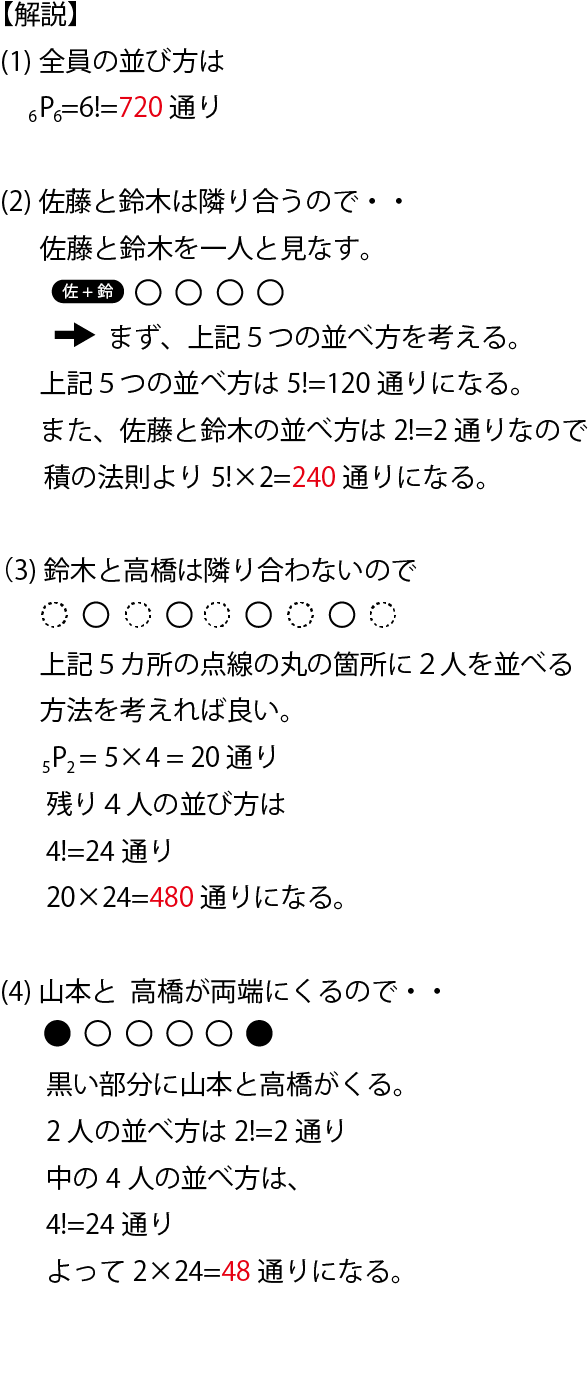



高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




spi非言語の問題を1分以内に解く 場合の数 順列 組み合わせ の練習問題 テストセンター Webテスト ペーパーテスト 模擬試験のspi検査対策 もう塾や予備校は不要 Youtube



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




場合の数 これだけは覚えよう 並べる と 選ぶ の計算方法の違い 中学受験ナビ




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




中学数学 場合の数




この問題はなぜ順列の公式ではなく 組み合わせの公式で説いているのですか Clearnote




高校数学無料問題集 数a 第1章 場合の数と確率 組合せ 桝 ます Note




苦手でも分かる 順列 P と組み合わせ C の使い分け 確率 ともよし塾 受験と科学の解説授業



場合の数の一般問題 京極一樹の数学塾




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




場合の数 番外編 順列p 組合せc 教遊者




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学




場合の数20 重複順列 怜悧玲瓏 高校数学を天空から俯瞰する




3講 順列 1章 場合の数と確率 問題集 高校数学a



1




高校数学a 組分け問題全パターン 受験の月




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




3講 順列 1章 場合の数と確率 問題集 高校数学a



場合の数の一般問題 京極一樹の数学塾




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長




高校数学 数a 17 組合せ 道順編 Youtube




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学
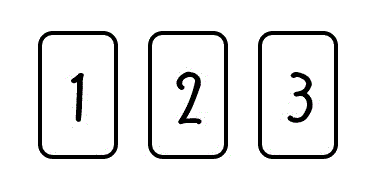



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube
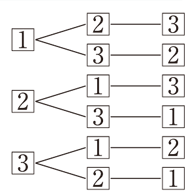



順列と組み合わせ 算数用語集



Spi練習問題 Com



順列と組み合わせの違いと見分け方 公式や練習問題 受験辞典




Spi 場合の数 最速解法 例題 Study Pro Spi




順列の問題 一定の条件で並べる 高校数学の知識庫



同じものを含む順列の問題 京極一樹の数学塾
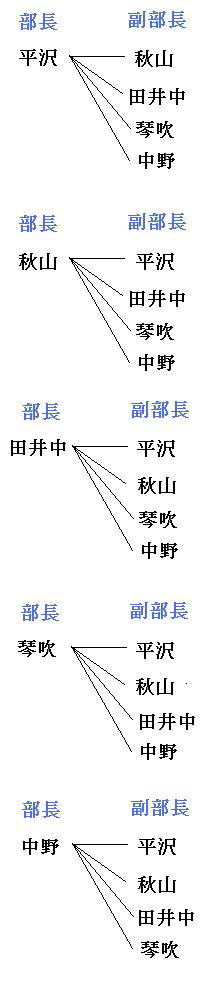



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ


